A Practical Guide to Gradient Boosted Trees - Part I, Regression
 MartinLiebig
Administrator, Moderator, Employee, RapidMiner Certified Analyst, RapidMiner Certified Expert, University Professor Posts: 3,510
MartinLiebig
Administrator, Moderator, Employee, RapidMiner Certified Analyst, RapidMiner Certified Expert, University Professor Posts: 3,510 Gradient Boosted Trees are one of the most powerful algorithms for classification and regression. They have all advantages of trees including the strength of handling nominal data well. The downside of any powerful, multivariate method is its complexity. This is the first of a series of articles drilling down into the algorithms and explain how they work.
The Setting
In this tutorial we will investigate how a Gradient Boosted Tree is doing a regression. As training data we use a sqrt-function between 0 and 1.

To make our algorithm easier more graspable we use a few simplifications. We do a regression for a label variable (y) with only one dependet variable (x).
We do use a GBT with a depth of 1 and learning rate of 1. We will discuss these options in later articles in more depth.
Initialization
Before starting with the real algorithm we will set a base line prediction. Our whole algorithm will consist of a lot of steps. The resulting function f(x) which will approximate the sqrt-function is a sum of the results of the individual steps. The first step is slightly different. We do set the base line prediction f0 to the average label. In our data this is 0.667.
Now we can move to the first iteration.
Step 1 - Calculate Errors
As a first step we calculate the errors. In our case these are the residuals between or our previous prediction f(x) and the truth y. In our fist iteration we do have f(x) = f0 = 0.667.
We define r = y - f(x) as the error for each individual example. It is crucial to note that the tree in each iteration is not predicting the label, but r! Since this is only a change in scale our sqrt-function still looks like this:
Step 2 - Tree Building
We now built a regression tree predicting r. Since we limit our tree to a depth of one we get: 
This tree results in two leafs. We call this leafs R11 and R12 representing the first and the second leaf in the first iteration. For each of the two leafs we need to find the best prediction.
Step 3 - Prediction Definition
In our regression problem the calculation of what we predict in the leafs is fairly straight forward. We want to find the prediction, which minimizes the difference between our function and the truth. In our case this is the average of r in each leaf. We define the prediction in the i-th iteration and the j-th leaf as gij and get for our data:
g11 = -0.254
g12 = +0.157
Step 4 - Update of our Function
We can now update our approximated function to estimate y, called f(x). Let's define the result of our first iteration f1:
f1 = -0.254 if x < 0.382, else: +0.152
And f(x) = f0 + f1. This results in a total function which approximates our initial unscaled sqrt like this:
 Step 1 - Part 2, Build residuals again
Step 1 - Part 2, Build residuals again
We can now do Step 1 again. But this time we build the residuals between our new function approximation f(x) = f1 + f2 and y. So we get a picture like this: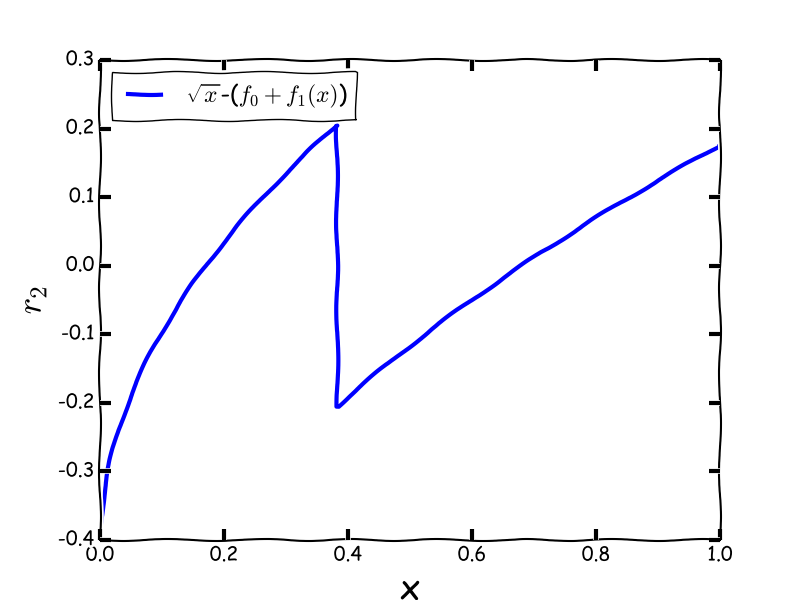
In this iteration of the algorithm we try to fit this functions of residuals to get a better overall function approximation.
Step 2 and 3- Part 2, Build the tree and calculate a prediction.
Again we built a tree which splits up our data into to parts. If you look at the picture above, we do search for the point on the x-axis, where we can draw two lines parallel to the a-axis, which have a minimum distance to the residuals.
The tree is telling us, that the splitting point is performed at 0.107 and the two parallel lines g21 and g22 are -0.193 and +0.023.


Step 4 - Updating the function
The last step is to update our function. It is now:
f(x) = f0 + f1+f2
or in full words:
f1 = 0.667
-0.254+ if x < 0.382
+0.152 if x >= 0.382
- 0.193 if x < 0.107
+ 0.023 if x >= 0.107
Or in a drawn form it looks like this:
Please be aware that the second tree is also raising the right hand side of the function by a little bit.
With this knowledge we can now move on and start with Step 1 again. That's it.
Naming
- y is the value of the label. E.g. the true value you want to predict
- x is the dependent variable. E.g. one (or many) regular attributes
- f(x) is the derived formula to predict y. E.g. the model
- Rij is the j-th leaf in the i-th iteration of the algorithm.
- gij the constant added to our function for all examples who are in the i-th iteration and the j-th leaf. Note: Often called gamma in literature.
Dortmund, Germany


Comments
Thank you for a very helpful step-by-step explaination of the GBT algorithm!
Is there any typos in the last step (Step 4 - Updating the function)? Why do the conditions overlap (x<0.382 and x<0.107)? Could you explain more on how to determine a position to do a split (as at x= 0.382 and x= 0.107), or how f1 and f2 are built?
thank you for the interesting guide how Gradient Boosted Trees work. Very interesting!
You wrote the following:
Does this mean that the prediction of the respective r is considered in each iteration to calculate the overall performance (avg(r's in each iteration)) which is finally displayed by the Performance Vector?
Or does the Performance Vector represent the r prediciton in the final improved state of the tree?
Thank you in advance for your feedback!
Best regards,
Fatih
Dortmund, Germany