Linear model coefficients into prediction confidence
 kypexin
Moderator, RapidMiner Certified Analyst, Member Posts: 291
kypexin
Moderator, RapidMiner Certified Analyst, Member Posts: 291  Unicorn
Unicorn
Hi miners,
The question might seem weird, but. I rare use linear models, but should use more!
Is there any obvious way to build an equation from linear model coefficients that would derive binominal label prediction confidence?
I am applying GLM to the dataset which contains polynominal attributes which were derived from discretizing numericals by enthropy to get ranges. Also there is a binominal label. If for example I initially had one variable named 'total_changes', at the end I have this kind of attributes and their coefficients:
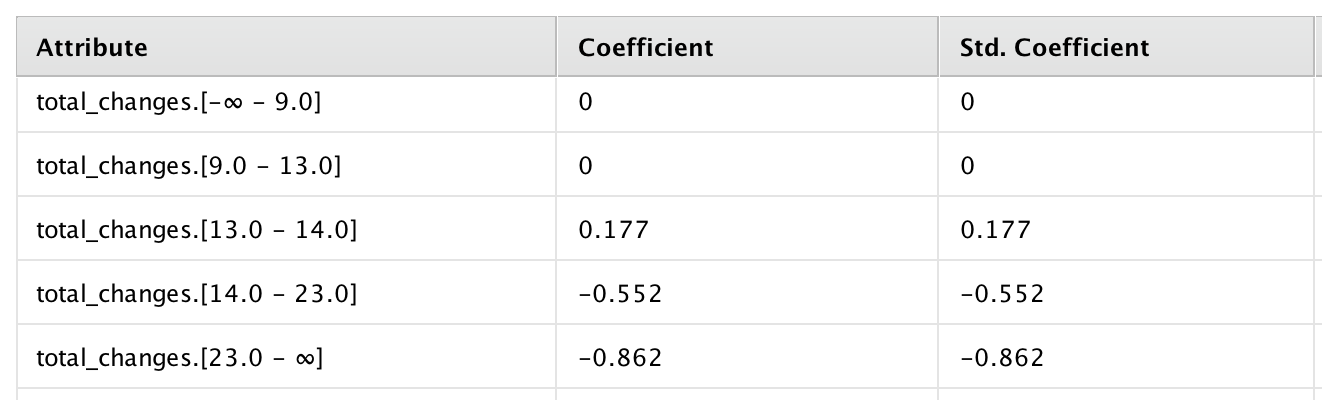
So this should be interpreted that total_changes between 13 and 14 adds to the confidence, while over 14 negatively impacts it, while less than 13 has no effect on it. Same with other variables.
So, question is, is it possible to make an equation from this coefficients, which, given the ranges of variables, would calculate the confidence between 0 and 1? Or maybe any other way to make a meaningful equation which can be applied to new unseen data?
Thanks.
Best Answer
-
Options
 earmijo
Member Posts: 270
earmijo
Member Posts: 270  Unicorn
Unicorn
Yes, you can.
The coefficients RM reports are for the log-odds :
y* = Log ( p / (1-p) ) = b0 + b1*x1 + b2*x2 + ... + bk*xk
p = probability of success
Once you have y*, getting p is easy:
p = exp(y*)/( 1+ exp(y*))
My question for you: Why would you want to discretize? It's a waste of information. Why not include the variable directly in the equation?
2


Answers
Wow thanks @earmijo! Would evaluate this closely.
Question for a question, answer for an answer
1) b0 + b1*x1 + b2*x2 + ... + bk*xk ==> do I get it right that in case of discretized features like mine (on a previous screenshot) those 'xk' are just eliminated (I mean, are equal to 1), and the equation is just a sum of intercept and coefficients, except if a numerical feature is present?
2) Why do I discretize, it is a good question indeed. It turns out that without discretization the performance of the model drops. This happens because of the specific nature of the data (it represents fraud cases), so an analysis uncovered pretty stable patterns where actual fraud cases tend to gather. Also remember, I discretize by entropy on labeled data so some of those ranges would represent stable good areas and some stable bad areas. This is why I decided to use ranges instead of continuous variables.
Vladimir
http://whatthefraud.wtf
@kypexin wrote:
Wow thanks @earmijo! Would evaluate this closely.
Question for a question, answer for an answer
1) b0 + b1*x1 + b2*x2 + ... + bk*xk ==> do I get it right that in case of discretized features like mine (on a previous screenshot) those 'xk' are just eliminated (I mean, are equal to 1), and the equation is just a sum of intercept and coefficients, except if a numerical feature is present?
Exactly. In your case, after discretizing Total.changes becomes a categorical variable and RM will create a set of dummy variables. Only one can be different from zero. So you will get:
Log Odds = Log ( p / (1-p) ) = Intercept + Bj * (1) = Intercept + Bj
RM will typically drop one of the categories (because it is redundant). For that case in particular,
Log Odds = Log( p / (1-p) ) = Intercept
(I'm assuming there are no other regressors. If there are you add them to the equation multiplied by their betas.
For instance I ran a very simple logistic regression of Subscription (Yes/No) vs Age and Discretize it as you did. I get:
Log Odd = Log ( p / (1-p) ) = -14.89 +14.25 *[Age in 31-34] + 17.69*[Age 34+]
If you want predictions for customers ages 29, 32.5, 40, you would get
Case AGe = 29
Log Odds = -14.89 + 14.25(0) + 17.69(0)
Prob Subscription = 3.4 * 10^-7
Case Age = 32.5
Log Odds = -14.89 + 14.25(1) + 17.69(0)
Prob Subcription = 0.34
Case Age = 40
Log Odds = -14.89 + 14.25(0) + 17.69(1)
Prob Subscription = 0.94
I'm attaching an excel sheet with the calculations.
Thanks a lot @earmijo
Last thing, maybe you know how the intervals interpreted, as they are notated all in square brackets?
Like, [9-13] and [13-14] and [14-19]. Is 13 in the first or second one?
I would logically expect that left boundary is included and right is excluded, so [9-13] makes 9 to 12 and [13-14] makes 13.
But then saw these 4 ranges in another variable and seems it should be the other way around, because:
[-∞ - 0.0] <-- we cant exclude zero from this one, so : 0
[0.0 - 1.0] : 1
[1.0 - 3.0] : 2 to 3
[3.0 - ∞] : 4 to infinity
Is that correct?
Vladimir
http://whatthefraud.wtf
It looks like :
[a,b] means (a,b]
i.e. a is outside the interval, b is inside.