Options
Automatic feature engineering: results interpretation
Hi there,
I played a bit with automatic feature engineering operator and I would like to get some points cleared; specifically, how do I interpret the result.
I have used 'balance for accuracy' = 1 and 'feature selection' option (no generation) on a dataset of 14,000 examples / 142 regular features, split 80/20 for train and test. Inside feature selection operator I used GLM learner on a numeric label (so, we have a linear regression here) and RMSE criteria for optimization.
This is the output I got in progress dialog:
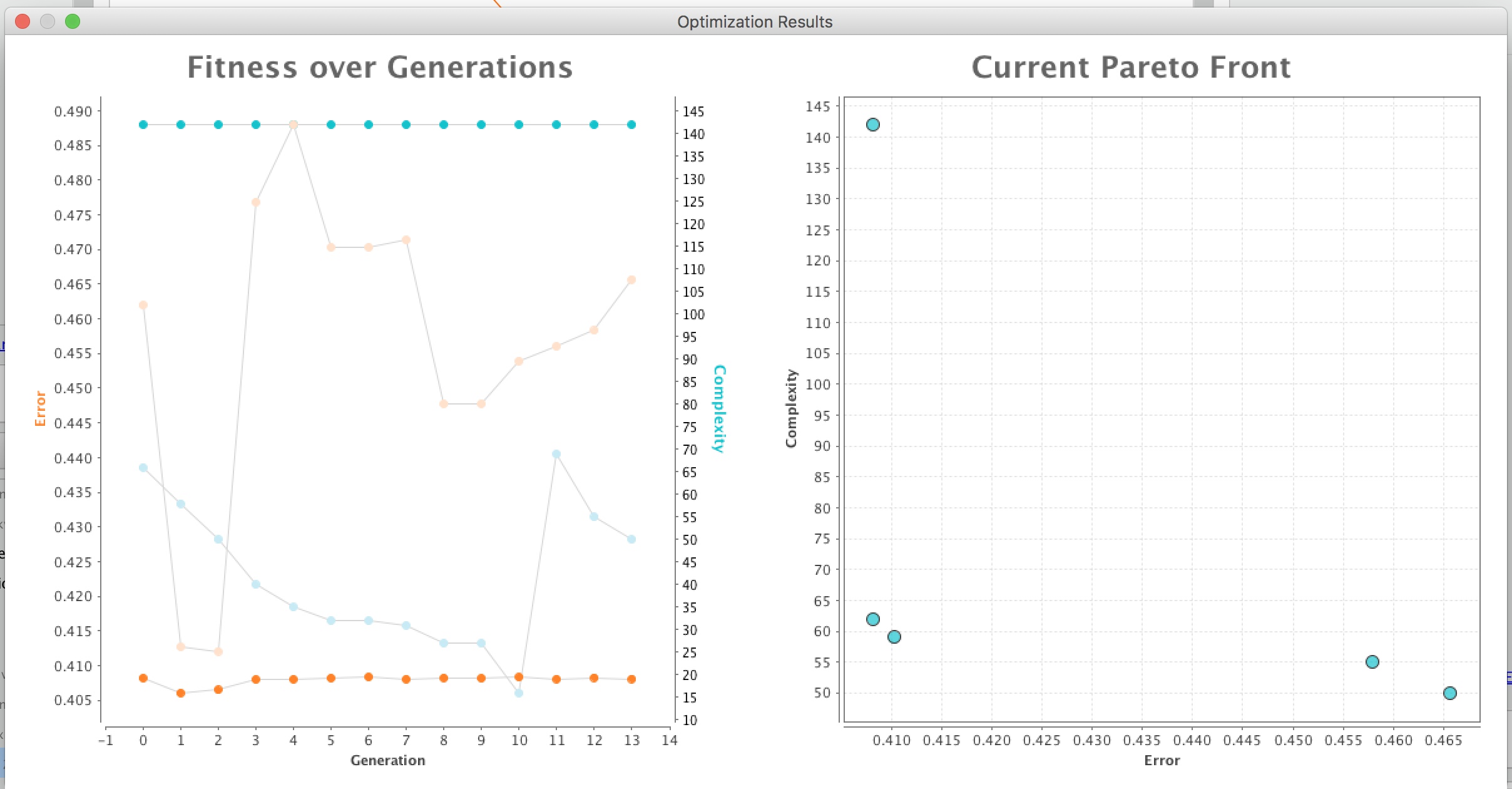
In total, 5 feature sets were generated, with these fitness / complexity correspondingly:
0.408 / 142
0.408 / 62
0.410 / 59
0.458 / 55
0.466 / 50
So far, in terms of RMSE minimization, first two sets are optimal (leftmost points on the right graph). However, the first one is also identical to original set, which means ALL features were used.
I played a bit with automatic feature engineering operator and I would like to get some points cleared; specifically, how do I interpret the result.
I have used 'balance for accuracy' = 1 and 'feature selection' option (no generation) on a dataset of 14,000 examples / 142 regular features, split 80/20 for train and test. Inside feature selection operator I used GLM learner on a numeric label (so, we have a linear regression here) and RMSE criteria for optimization.
This is the output I got in progress dialog:

In total, 5 feature sets were generated, with these fitness / complexity correspondingly:
0.408 / 142
0.408 / 62
0.410 / 59
0.458 / 55
0.466 / 50
So far, in terms of RMSE minimization, first two sets are optimal (leftmost points on the right graph). However, the first one is also identical to original set, which means ALL features were used.
- Why optimization operator still have chosen the bigger set (142) not the smaller (62), as the fitness is equal for both?
- Is there a way to make optimizer choose the most optimal set AND the smallest at the same time, in the situation like above?
- If the most accurate feature set includes all the features, does it mean that they all are contributing to predictions, so no feature can be removed without increasing the error?
- How do I interpret the left graph? I understand it shows trade-offs for error vs. complexity for different feature sets, but how exactly do I read it? Why the upper line (in blue) shows complexity 142 and error close to 0.490 (logically it's the highest error, so the 'worst' option)? On the contrary, lower line (in orange) goes around 0.408 (lowest value) but complexity is around 20? In other words, I cannot find analogy between left and right charts.
Tagged:
0
Best Answer
-
Options
 IngoRM
Administrator, Moderator, Employee, RapidMiner Certified Analyst, RapidMiner Certified Expert, Community Manager, RMResearcher, Member, University Professor Posts: 1,751
IngoRM
Administrator, Moderator, Employee, RapidMiner Certified Analyst, RapidMiner Certified Expert, Community Manager, RMResearcher, Member, University Professor Posts: 1,751  RM Founder
Hi,On questions 1 and 2:I think @lionelderkrikor is right, there will be tiny differences which is the reason why the original one was picked. In fact, if the accuracy would be exactly the same, the Pareto optimal result would be the feature set with 62 (since it dominated the other one).I would recommend trying a balance factor of 0.7 or 0.8 and you will likely get one of the results with 59 or 62 features. In my own experience, I often do not want to optimize accuracy really with feature selection but get similar accuracy with smaller data sets (which makes training and scoring faster and the model less complex and more robust). So I often end up picking a model in the 0.7 to 0.95 range...Question 3:Yes, most of them will contribute. Obviously that depends a bit on the number of individuals during the optimization. You can make the settings manually (increase the number of individuals to 100 or so but reduce the number of generations, otherwise it may run for ages...). This will likely give you a more complete picture if really (almost) all features are necessary.Question 4:The best idea is to ignore the graph altogether :-) We actually considered to remove it. It was kind of useful while we have been tweaking some of the optimization heuristics, but it really is not that interesting in my opinion for users. Anyway, here is what the chart tells you: for each generation, it tells you the highest and the lowest error rate of all individuals of this generation's population. Same is true for the complexities: it shows the highest and the lowest complexity for the generation's population. Since there are more individuals in each population than the Pareto-optimal solutions shown on the right, there does not have to be a 1:1 relationship between both charts.Towards the end of the optimization, however, there typically is one. Have a look at the 4 points at the far right end (last generation). The best error is 0.408 (dark orange) and the worst one is 0.465 (light orange). Those are the points at the left and the right end of the Pareto front on the right. At the same time, you can see the highest complexity is 142. This is shown in dark blue which at the end of the optimization typically corresponds to the best performing feature set (which is why they share the dark color). And last but not least there is the lowest complexity (50, light blue). Which at the end of the run typically corresponds with the worst feature set with respect to error rate, hence the light color for both.Hope this helps,Ingo11
RM Founder
Hi,On questions 1 and 2:I think @lionelderkrikor is right, there will be tiny differences which is the reason why the original one was picked. In fact, if the accuracy would be exactly the same, the Pareto optimal result would be the feature set with 62 (since it dominated the other one).I would recommend trying a balance factor of 0.7 or 0.8 and you will likely get one of the results with 59 or 62 features. In my own experience, I often do not want to optimize accuracy really with feature selection but get similar accuracy with smaller data sets (which makes training and scoring faster and the model less complex and more robust). So I often end up picking a model in the 0.7 to 0.95 range...Question 3:Yes, most of them will contribute. Obviously that depends a bit on the number of individuals during the optimization. You can make the settings manually (increase the number of individuals to 100 or so but reduce the number of generations, otherwise it may run for ages...). This will likely give you a more complete picture if really (almost) all features are necessary.Question 4:The best idea is to ignore the graph altogether :-) We actually considered to remove it. It was kind of useful while we have been tweaking some of the optimization heuristics, but it really is not that interesting in my opinion for users. Anyway, here is what the chart tells you: for each generation, it tells you the highest and the lowest error rate of all individuals of this generation's population. Same is true for the complexities: it shows the highest and the lowest complexity for the generation's population. Since there are more individuals in each population than the Pareto-optimal solutions shown on the right, there does not have to be a 1:1 relationship between both charts.Towards the end of the optimization, however, there typically is one. Have a look at the 4 points at the far right end (last generation). The best error is 0.408 (dark orange) and the worst one is 0.465 (light orange). Those are the points at the left and the right end of the Pareto front on the right. At the same time, you can see the highest complexity is 142. This is shown in dark blue which at the end of the optimization typically corresponds to the best performing feature set (which is why they share the dark color). And last but not least there is the lowest complexity (50, light blue). Which at the end of the run typically corresponds with the worst feature set with respect to error rate, hence the light color for both.Hope this helps,Ingo11


 Unicorn
Unicorn
Answers
It's just to submit a hypothesis to the 1. question :
You have set "Balance for accuracy" = 1 , so RM will select the most accurate feature set :
Maybe the fitness with 142 features is something like 0,407777... and it is effectively less than the fitness
with 62 features (maybe something like 0,4079999999....)....
Regards,
Lionel
I am always forgetting about this real numbers rounding thingy. And all other explanations seem pretty straightforward, so I am now more confident in automatic feature engineering results interpretation.
Vladimir
http://whatthefraud.wtf