Time Series Extension new version 0.1.2 with ARIMA Trainer, Moving Averages, and more...
 sgenzer
Administrator, Moderator, Employee, RapidMiner Certified Analyst, Community Manager, Member, University Professor, PM Moderator Posts: 2,959
sgenzer
Administrator, Moderator, Employee, RapidMiner Certified Analyst, Community Manager, Member, University Professor, PM Moderator Posts: 2,959 
[copied from blog post 17 Oct 2017 by @tftemme]
Time Series Extension (Marketplace).
In this post I want to give you a short overview over the features already provided in the alpha version 0.1.2.
 Figure 1: Image of the Time Series Extension Samples folder in the RapidMiner Repository panel after the installation of the Time Series Extension.
Figure 1: Image of the Time Series Extension Samples folder in the RapidMiner Repository panel after the installation of the Time Series Extension.
Time Series Extension Samples Folder
After downloading the extension from the marketplace it adds a new folder, called Time Series Extension Samples Folder to your repository panel. It contains some time series data sets and some process templates to play around with.
I will also use these data sets and variations of the template processes to demonstrate the features of the Time Series Extension in this blog post.
The processes shown in this post are also attached to the post, so you can try them out for yourself if you want.
Moving Average Filter
The first Operator I want to show is the Moving Average Filter. To demonstrate its purpose, I want to analyse the 'Lake Huron' data set. It describes the surface levels of Lake Huron (Wikipedia) in the years 1875 - 1972.
When you load the data from the Samples folder (red line in figure 2) you can see that the surface level shows some variation at different scales. There are some time windows with high and with low surface levels. But there are also small variations where noisy data can be seen.
To smooth this data a bit we can use the Moving Average Filter Operator. The Moving Average Filter calculates the filtered values as the weighted sum of values around the corresponding value. The weights depend on the type of the filter. Currently three different types are supported: "SIMPLE, "BINOM, and "SPENCERS_15_POINTS".
For "SIMPLE" weighting the weights are all equal. This filter is also known as a rolling mean, rolling average, or similar terms. The result is shown as the blue line in figure 2.
 Figure 2: Result view of the Lake Huron data set. The original data (red line) and the result of a SIMPLE Moving Average Filter (blue line) are shown.
Figure 2: Result view of the Lake Huron data set. The original data (red line) and the result of a SIMPLE Moving Average Filter (blue line) are shown.
The smoothing effect is cleary visible, but also less evident features such as the removal of the large spike in the year 1929 from the filtered data. The "BINOM" filter type could improve the filtering.In the case of this filter type the weights follows the expansion of the binomial expression (1/2 + 1/2s)^(2q). For example, for q = 2 the weights are [1/16, 4/16, 6/16, 4/16, 1/16].
For a large filter size the weights approximate to a normal (Gaussian) curve. This filter type is capable of smoothing the data, but preserving more features in the data. The result is shown in figure 3.
 Figure 3: Result view of the Lake Huron data set. The original data (red line) and the result of a BINOM Moving Average Filter (blue line) are shown.
Figure 3: Result view of the Lake Huron data set. The original data (red line) and the result of a BINOM Moving Average Filter (blue line) are shown.
The third filter type (SPENCERS_15_POINTS) is a special filter and not applicable for this use case.
ARIMA
In many use cases we not only want to analyse historic data, but also want to forecast future values. Therefore we can use an ARIMA model (Wikipedia) to predict the next values of a time series which is described by this model.
For example we can use the ARIMA Trainer Operator to fit an ARIMA model to the time series values of the Lake Huron data set. For now we use the default parameters of the ARIMA Trainer Operator: p = 1 autoregressive terms and q = 1 moving average terms.
Figure 4 shows the RapidMiner process (including the above described Moving Average Filter Operators).
 Figure 4: RapidMiner process to analyse the Lake Huron data set. The two Moving Average Filter Operators are included as well as the fitting of the ARIMA model and the forecasting of the next 10 years of the data set.
Figure 4: RapidMiner process to analyse the Lake Huron data set. The two Moving Average Filter Operators are included as well as the fitting of the ARIMA model and the forecasting of the next 10 years of the data set.
The Apply Forecast Operator calculates the forecasted values of the next 10 years. The result of the forecast and the original ExampleSet (containing the original data and the filtered data) are joined together and delivered to the result port.
Figure 5 shows the original Lake Huron data (red line) and the forecasted values (blue line).
 Figure 5: Result view of the Lake Huron data set. The original data (red line) and the result of the forecast (blue line) using the ARIMA model are shown.
Figure 5: Result view of the Lake Huron data set. The original data (red line) and the result of the forecast (blue line) using the ARIMA model are shown.
Differentation
To demonstrate the usage of the Differentation Operator I use the Monthly Milk Production data set from the Time Series Extension Samples folder. The data is visualized in figure 6 (red line).
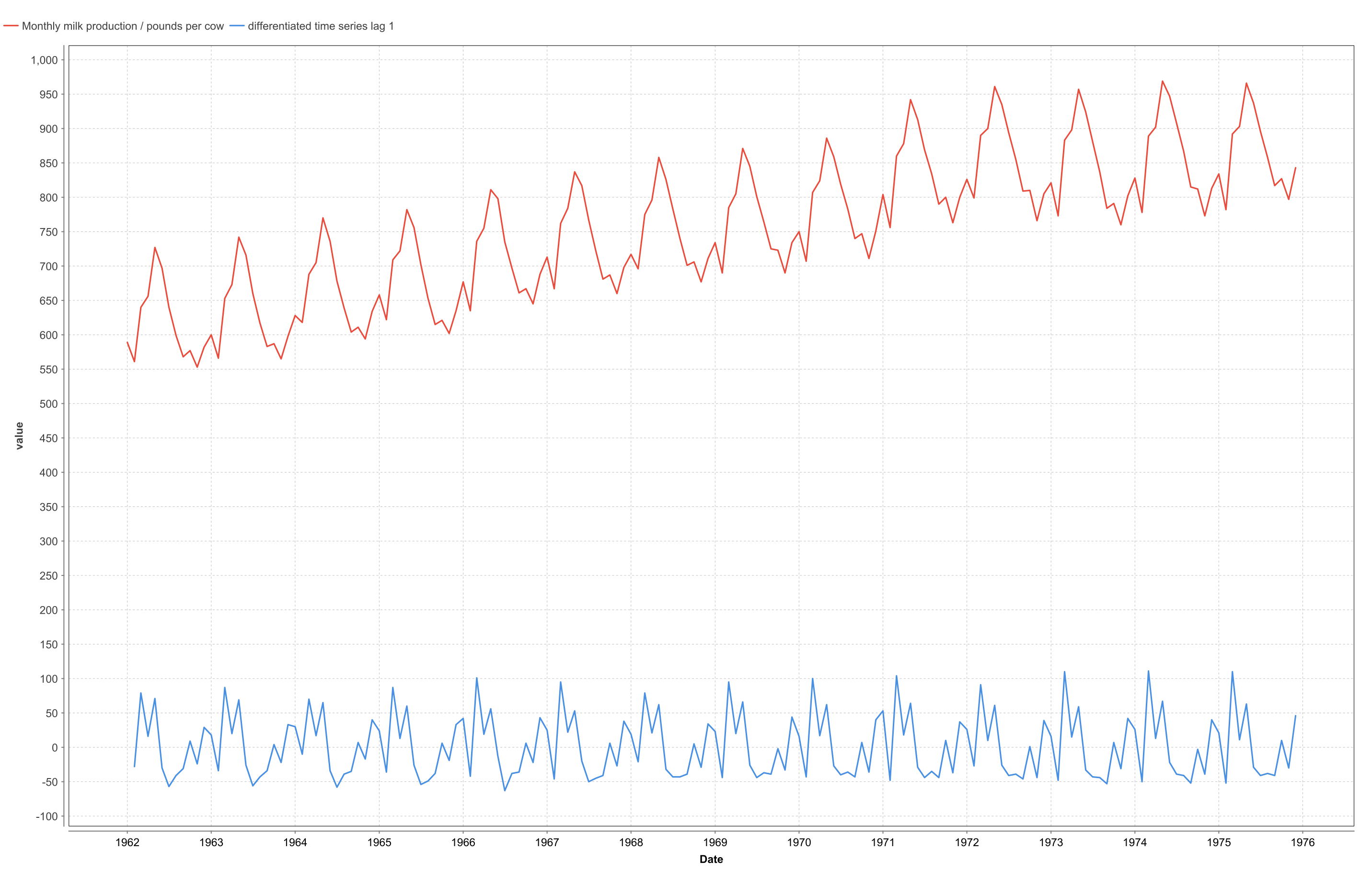 Figure 6: Result view of the Monthly Milk Production data set. The original data (red line) and the result of a Differentation Operator with lag = 1 (blue line) are shown.
Figure 6: Result view of the Monthly Milk Production data set. The original data (red line) and the result of a Differentation Operator with lag = 1 (blue line) are shown.
It is clearly visible that there is a seasonal variation in the data. Also the milk production increases from 1962 to 1972 and stays roughly on the same level since then.
If we are interested in the increase of the milk production itself, we can use the Differentation Operator to differentiate the data.The result (with the parameter lag set to 1) is also shown in figure 6 (blue line). Again the data is dominated by the seasonality, so it is hard to find time windows where the increase in milk production changes its behavior.
At this point the parameter lag can be used. The Differentation Operator calculates the new values as y(t+lag) - y(t). So with lag = 1 we calculate the increase from month to month. If we use lag = 12 we calculate the increase from one month to the same month next year, removing the seasonality in the differentiated data. The result is shown in figure 7 (red line).
 Figure 7: Result view of the differentiated Monthly Milk Production data set. The Differentation was applied with a lag = 12, removing the seasonality from the data set.
Figure 7: Result view of the differentiated Monthly Milk Production data set. The Differentation was applied with a lag = 12, removing the seasonality from the data set.
We can now see that between 1963 and 1973 the yearly increase is roughly 15 pounds, with some time windows showing an even higher increase in 1964, 1967 and 1972. Also in the years 1973, 1974 and between 1975 and 1976 there is even a decrease in the monthly production.
So here the Differentation Operator gives us the possibility to remove seasonality from the data, to get a better overall picture of our data.
Additional Operators
In addition there are some more Operators provided by the Time Series Extension:
-
The Normalization Operator gives you the possibility to normalize your Time Series data.
-
The Logarithm Operator gives you the possibility to apply the natural or the common logarithm to your Time Series data.
-
The Generate Data (ARIMA) provides you with the possibility to simulate Time Series data, produced by an ARIMA model where parameters can be specified by the user.
-
The Check Equidistance Operator checks an Index Attribute of a Time Series data set if it is equidistance on a milli second level.
Figure 8 shows the RapidMiner process used to analyse the Monthly Milk Production data set. The above described Differentation Operators as well as a Normalization and a Logarithm Operator are used (the latter ones for demonstrating the application of the Operators).
 Figure 8: RapidMiner process to analyse the Monthly Milk Production data set. The two Differentation Operators are included as well as a Logarithm and a Normalization Operator.
Figure 8: RapidMiner process to analyse the Monthly Milk Production data set. The two Differentation Operators are included as well as a Logarithm and a Normalization Operator.
With this second process I end this blog post. In the next one I will go into detail about using the ARIMA Trainer and the Apply Forecast Operator and the possibility to combine this with one of the Optimize Operators.
Feel free to post every bug, usability problem, feature request or any feedback you have in the Product Feedback Area in the RapidMiner Community.
[Author @tftemme from RapidMiner Research]


Comments
I have some problems trying to download the processes that you attach.
I have installed the Time Series Extension and I can open the templates without any problem. And I can run it ok.
But when I can try to open your *.rmp files, then RapidMiner Studio doesn't recognize these operators.
I attach the errors with the two processes when I try to open it into RapidMiner Studio
Thank you.
Best regards,
Montse
And of course if you want to learn more about Time Series modeling in RapidMiner you can join my expert course on this topic, which will be running next on Mar 1st (see https://rapidminer.com/training/ )!
Lindon Ventures
Data Science Consulting from Certified RapidMiner Experts
Nothing to add here, thanks to @Telcontar120 . As said, the operators are now bundled with RM Studio and the operators in the processes of this thread do not work anymore. But you can use the ones from RM Studio to rebuild the processes I demonstrated here (which maybe a good lesson to get familiar with the operators).
Best regards,
Fabian
Thank you for your comments, @Telcontar120 and @tftemme.
Best Regards,
Montse